Анализ и моделирование частичных разрядов в изоляции высоковольтного оборудования
Видеозапись и стенограмма вебинара "Анализ и моделирование частичных разрядов в изоляции высоковольтного оборудования и кабелях как случайного импульсного процесса" от 12 октября 2017 года.
Лектор: Вадим Анатольевич Шахнин, доктор технических наук, профессор, Владимирский государственный университет имени А. Г. и Н. Г. Столетовых.
Стенограмма вебинара
Время чтения: 35 минут.
– Добрый день, уважаемые коллеги! Давайте начнём. Мы рады приветствовать вас на нашем новом вебинаре, посвящённом диагностике высоковольтного оборудования. Это уже второй вебинар из серии с Вадимом Анатольевичем Шахниным. У нас планируется насыщенная программа в рамках этой серии. Чтобы ничего не пропустить, пожалуйста, регистрируйтесь на все последующие вебинары по ссылке и следите за всеми новостями на нашем сайте. Отправляю ссылку в чат. Как я уже сказал, лектором выступает Вадим Анатольевич Шахнин, профессор кафедры электроэнергетики Владимирского государственного университета, доцент, доктор технических наук, автор более ста научных работ и 32 изобретений. Меня зовут Корытко Алексей, я являюсь администратором вебинаров, и буду отвечать на ваши сообщения в чате. Обязательно призываю вас активно участвовать в вебинаре, задавать свои вопросы, оставлять комментарии в чате. Перед тем как задать вопрос, пожалуйста, указывайте, к чему он относится: номер слайда или та или иная фраза лектора. По времени вебинар займёт около 40 минут, включая ответы на вопросы. На вопросы мы ответим в конце вебинара либо, если будет в этом необходимость, по ходу самого вебинара. На этом моё вступительное слово окончено. Давайте начнём. Вадим Анатольевич, здравствуйте!
– Здравствуйте, уважаемые коллеги! В качестве введения начну вебинар с общеизвестного. Мониторить состояние изоляции высоковольтного оборудования – является ключевым звеном в реализации внедряемого в настоящее время концепции обслуживания электросетевого оборудования на основе анализа его текущего состояния. Приверженность этой концепции подтверждена и в последних документах ПАО «Россети», в частности, в положении о единой технической политике в электросетевом комплексе, утверждённой советом директоров в феврале 2017 года. К числу перспективных методов мониторинга высоковольтного оборудования, безусловно, относится метод, основанный на анализе частичных разрядов. А сам процесс частичных разрядов подвержен влиянию множества факторов. Это и особенности структуры изоляции, уровень напряжённости электрического поля, его неоднородность, химический состав изолирующей среды и его изменения в процессе эксплуатации высоковольтного оборудования, наличие неоднородности посторонних предметов в изоляции, температура и т. д. Именно множество влияющих факторов и является предпосылкой целесообразности рассмотрения электрического шума, вызванного частичными разрядами как случайного импульсного процесса.
03:29
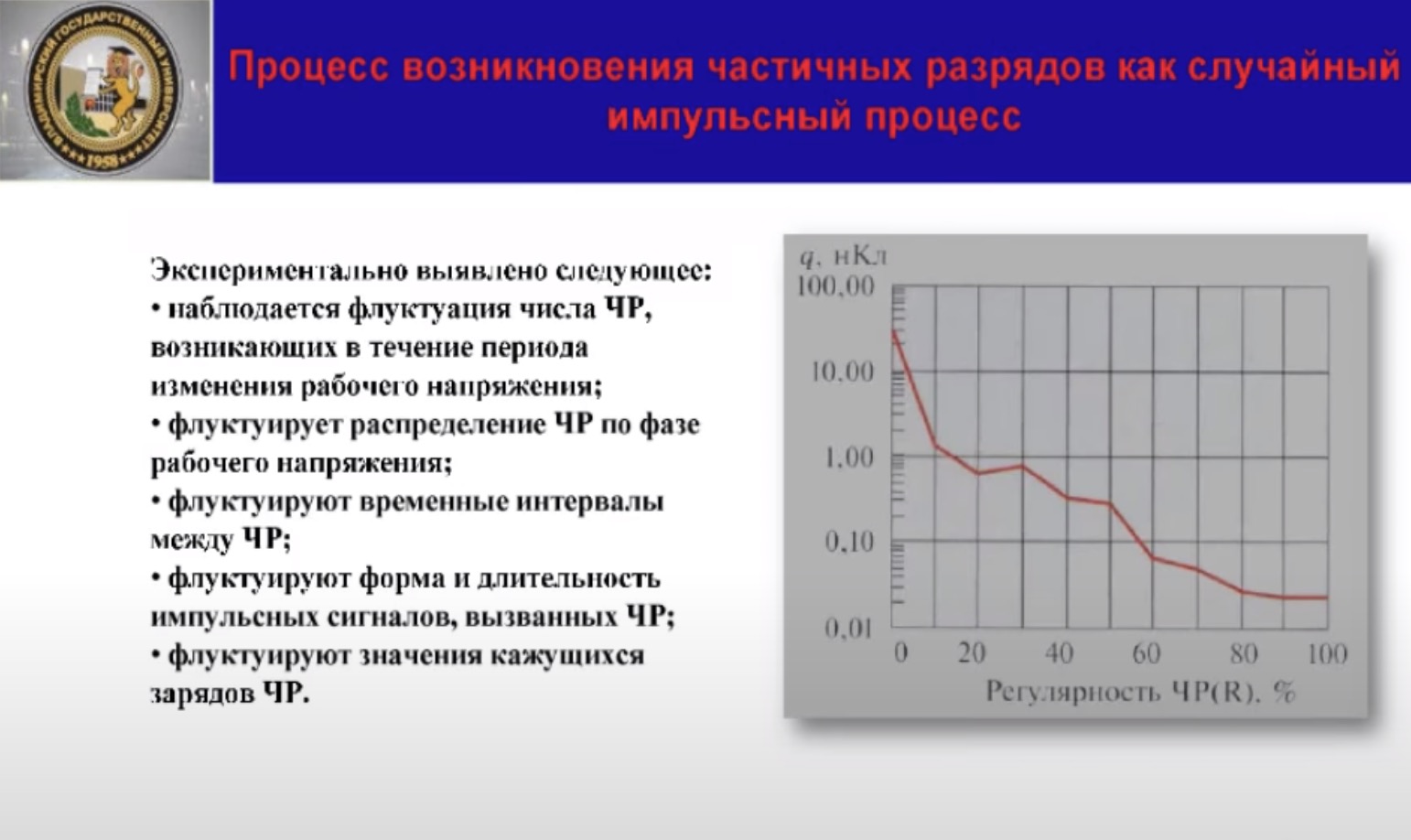
О случайном характере процесса свидетельствует исследование частичных разрядов в изоляции высоковольтного оборудования, находящихся под рабочим напряжением. Многочисленными экспериментами зарубежных специалистов и в нашей стране, направленных на исследование статистических характеристик частичных разрядов, установлено следующее. Наблюдается корреляция, флуктуация числа частичных разрядов в течение периода изменения воздействующего напряжения. Флуктурирует распределение частичных разрядов по фазе рабочего напряжения, флуктурируют временные интервалы между частичными разрядами, флуктурирует форма, длительность, амплитуда импульсных сигналов, вызванных ЧР, флуктурируют значения кажущихся зарядов частичных разрядов. В монографии ведущего специалиста в области диагностики высоковольтного оборудования методом частичных разрядов Василием Павловичем Удовико введено понятие регулярности частичных разрядов, которые трактуются автором как неустойчивость возникновения, а, по сути дела, случайный характер частичных разрядов. Регулярность частичных разрядов – это отношение числа импульсов, в которых зарегистрированы частичные разряды с кажущимся зарядом большего установленного уровня к общему числу периодов за определённый интервал времени.
05:04
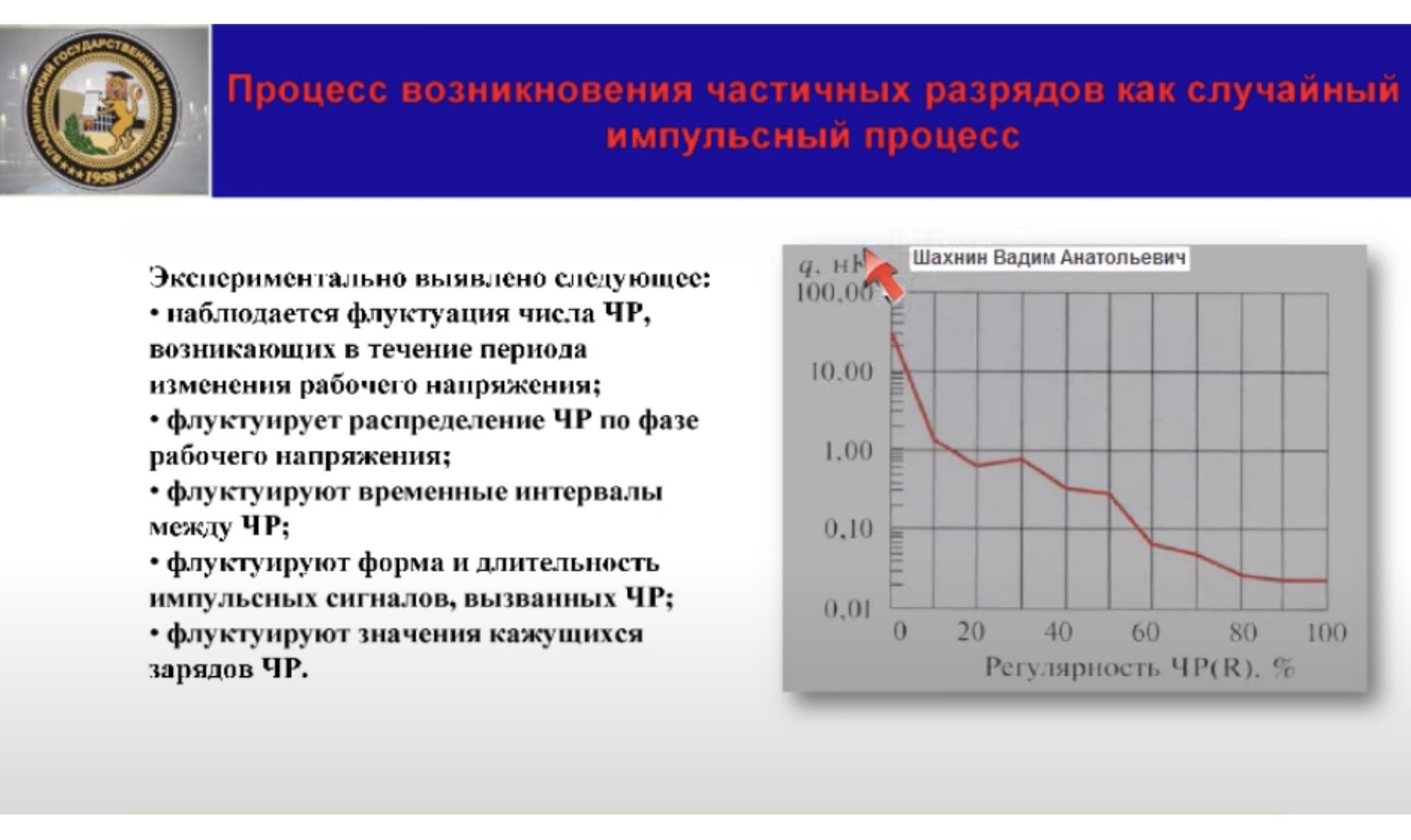
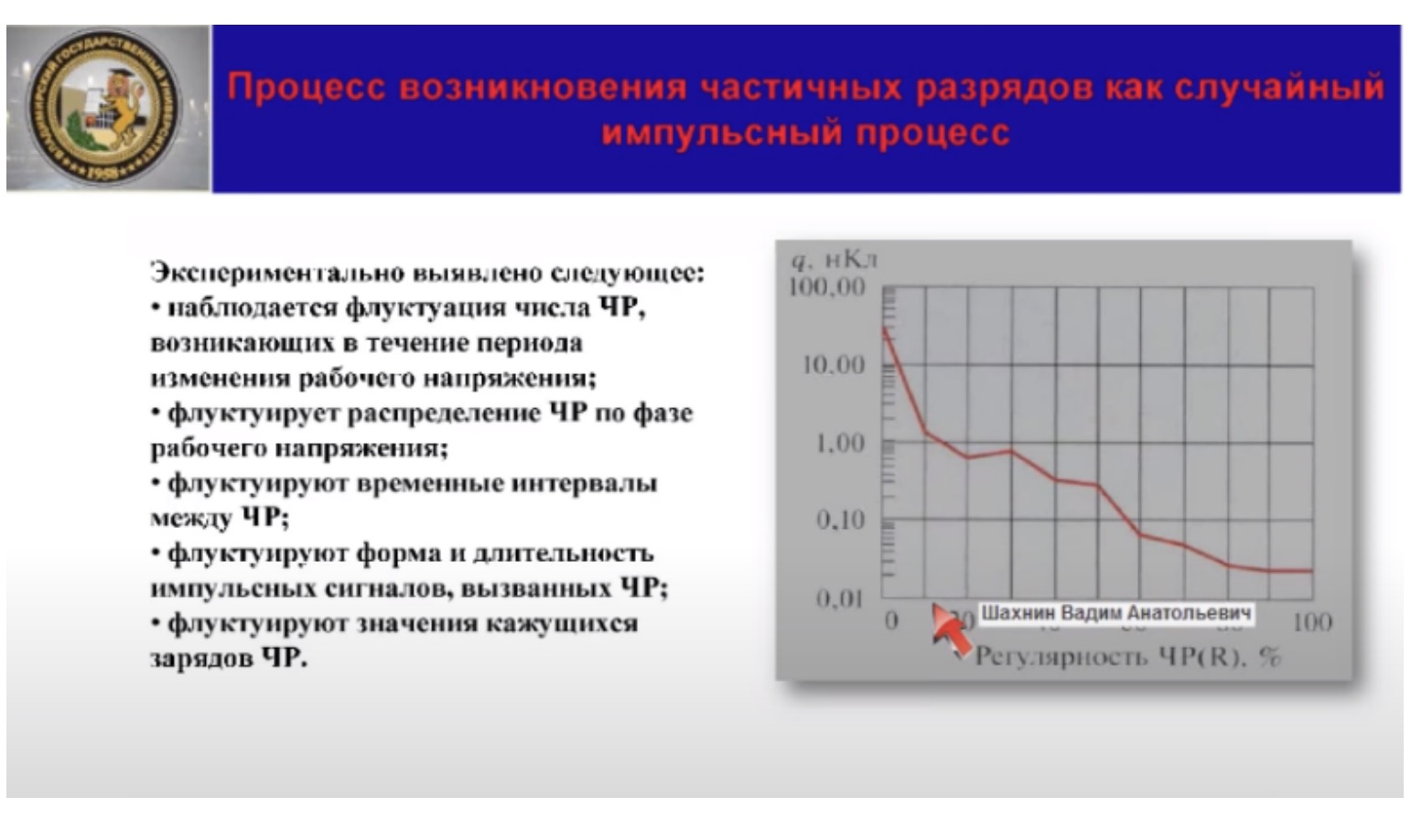
На рисунке этого слайда представлена кривая, связывающая между собой кажущийся заряд частичных зарядов и регулярность. Эта кривая получена Удовико и взята из его книги. Получена при диагностике высоковольтного двигателя, находящегося длительное время в эксплуатации. Трактовать эту кривую можно следующим образом
05:30
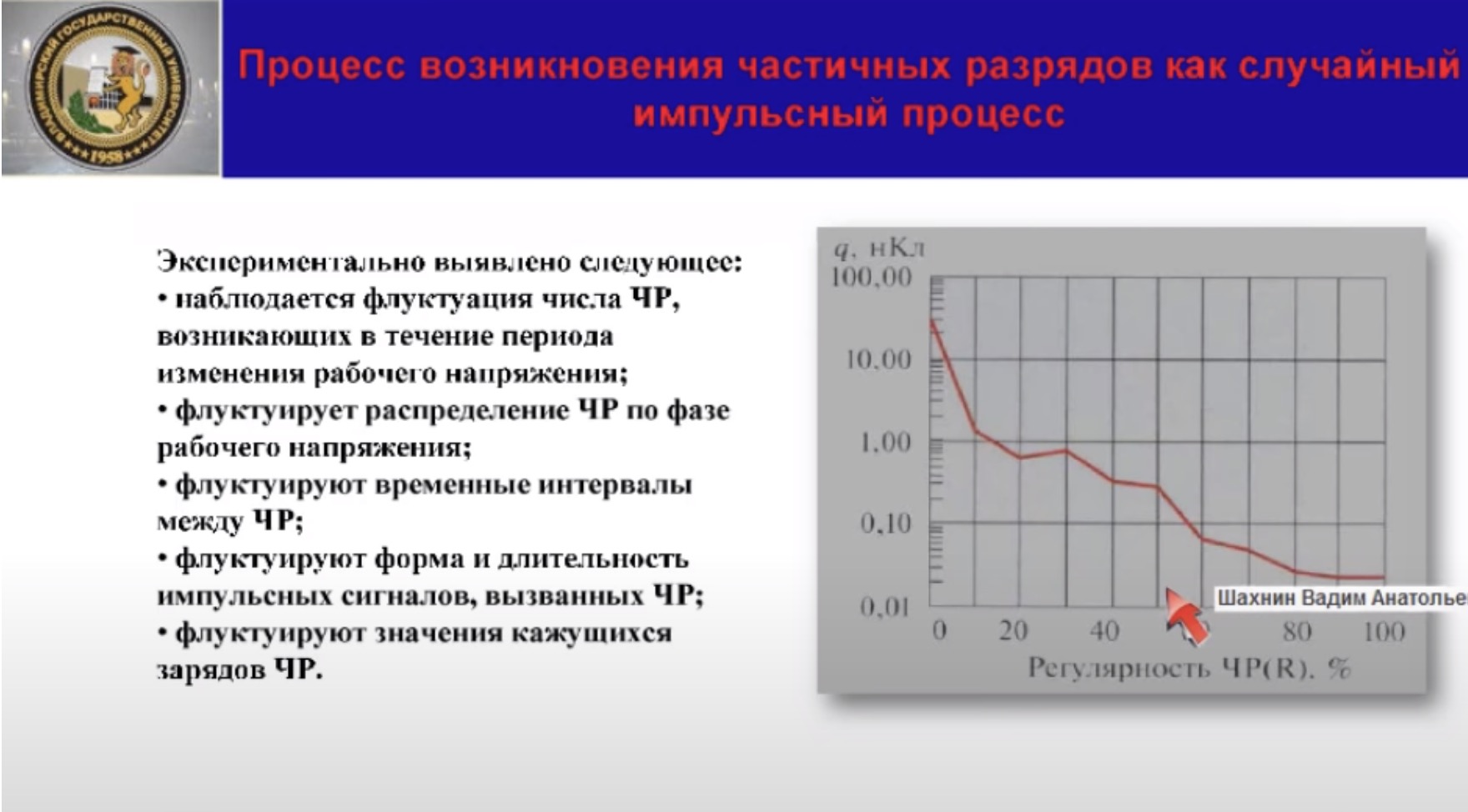
Например, вероятность появления частичных разрядов с кажущимся зарядом более 1 нКл составляет приблизительно 15%.
05:34
А вероятность появления частичного разряда с кажущимся зарядом порядка 500 пКл составляет около 55%.

05:44
Несмотря на общеизвестный случайный характер частичных разрядов, на многочисленные эксперименты по исследованиям статистических характеристик частичных разрядов в литературе, посвящённой диагностике высоковольтного оборудования, отсутствует систематическое описание частичных разрядов как случайного импульсного процесса. В значительной степени, по нашему мнению, это обусловлено отсутствием технических средств и методик исследования статистических характеристик частичных разрядов на работающем высоковольтном оборудовании под рабочим напряжением. Таким образом, теоретический анализ физических явлений, возникающих в изоляции высоковольтных аппаратов под действием электрического поля большой напряжённости, а также накопленный до настоящего времени большой экспериментальный материал позволяют сделать вывод о том, что процесс возникновения частичных разрядов с позиции теории вероятности целесообразно рассматривать, как стационарный и периодически не стационарный случайный импульсный процесс. Поэтому для анализа и математического описания моделирования частичных разрядов с целью диагностики высоковольтного оборудования целесообразно применить математический аппарат, который применяется как раз для описания случайных импульсных процессов. Кратко рассмотрим некоторые определения и теоремы, конечно, без доказательств, представляющих интерес для математического описания частичных разрядов.

07:22
Случайным импульсным процессом принято называть последовательность импульсов, параметры которых являются случайными величинами. В простейшем случае процесс представляет собой последовательность одинаковых по форме импульсов, имеющих случайные амплитуды и моменты возникновения. Функция ξ(t) описывает такой процесс. Вероятностные характеристики функции ξ(t) можно определить через вероятностные характеристики случайных величин: амплитуды av и времени момента возникновения случайного разряда tv . Если эти величины статистически независимы, то достаточно распределения вероятности этих величин для описания интересующего нас случайного процесса. Если вероятность появления импульса во временном интервале от t до t+Δt зависит только от длительности этого интервала, то вероятность появления n импульса в течение интервала T определяется распределением Пуассона.

08:52
В этом случае среднее значение случайной функции ξ(t) ,

09:19
описывающей интересующий наш случайный процесс, и автокорреляционная функция

09:24
определяется формулами 1 и 2.

09:30

09:32
В формуле 2 параметр t является временем корреляции, и корреляционная функция зависит именно от этого параметра, но не от времени t.

09:39
Если этот параметр стремится к 0, значение параметров процесса в начале и в конце интервала становится одинаковыми, а автокорреляционная функция обращается в дисперсию.

09:56
Из формул 2 и 3 видно, что среднее значение процесса ξ(t)

10:04
и дисперсия не являются функциями времени.

10:08
а автокорреляционная функция является функцией лишь интервала корреляции τ, но, опять же, не t.

10:15
Это позволяет отнести изучаемый нами процесс к стационарному. У стационарных процессов отмечу, что в случае вероятности характеристики не зависят от времени.

10:34
Для стационарных процессов введено понятие спектральной плотности, которое определяется, как преобразование Фурье от автокорреляционной функции. Это выражение 4.

10:50
Справедливо и обратное выражение 5.

10:52
Обратное преобразование устанавливает связь между спектральной плотностью g(ω) и автокорреляционной функцией.

11:02
Из этого следует вывод, это соответствие теореме Винера – Хинчина, что автокорреляционная функция и спектральная плотность в равной степени описывают случайные параметры случайного процесса.

11:38
Если у вас в распоряжении имеется ансамбль реализации случайного процесса, то спектральную плотность можно выразить через преобразование Фурье с помощью предела 6. Черта означает, что усреднение идёт по ансамблю множества реализаций.

12:04
По теореме о спектре свёртки для пуассоновского процесса справедливо выражение 10. Если длительность импульса является случайной величиной, а амплитуда и форма импульса являются детерминированными функциями. А если все три величины: амплитуда, длительность и форма импульса являются случайными функциями, то формула 10 преобразуется в формулу 11 путём введения усреднения по множеству реализаций.

12:48
Для большинства стационарных случайных процессов, в том числе для электрошумового процесса частичных разрядов, выполняется свойство эргодичности, заключающееся в том, что с вероятностью, близкой к единице, статистическое усреднение по множеству реализаций можно заменить усреднением по времени одной достаточно длинной реализации. Достаточным условием эргодичности стационарного процесса является приближение к 0 корреляционной функции при увеличении интервала корреляции. Это условие, которое представлено на слайде. Именно эргодичность стационарных случайных процессов позволяет производить аппаратные определения спектральной плотности и других характеристик случайных процессов. Случайный процесс изменения параметров частичных разрядов в реальной изоляции не может происходить с бесконечно большой скоростью. Значения параметров электрического состояния изоляции в разные моменты времени взаимосвязаны. Можно сказать, что ЧР-шум обусловлен частичными разрядами и обладает памятью, которая является отражением физико-химического состояния и свойств изоляции и определяет внутреннюю структуру этого случайного процесса.
14:19
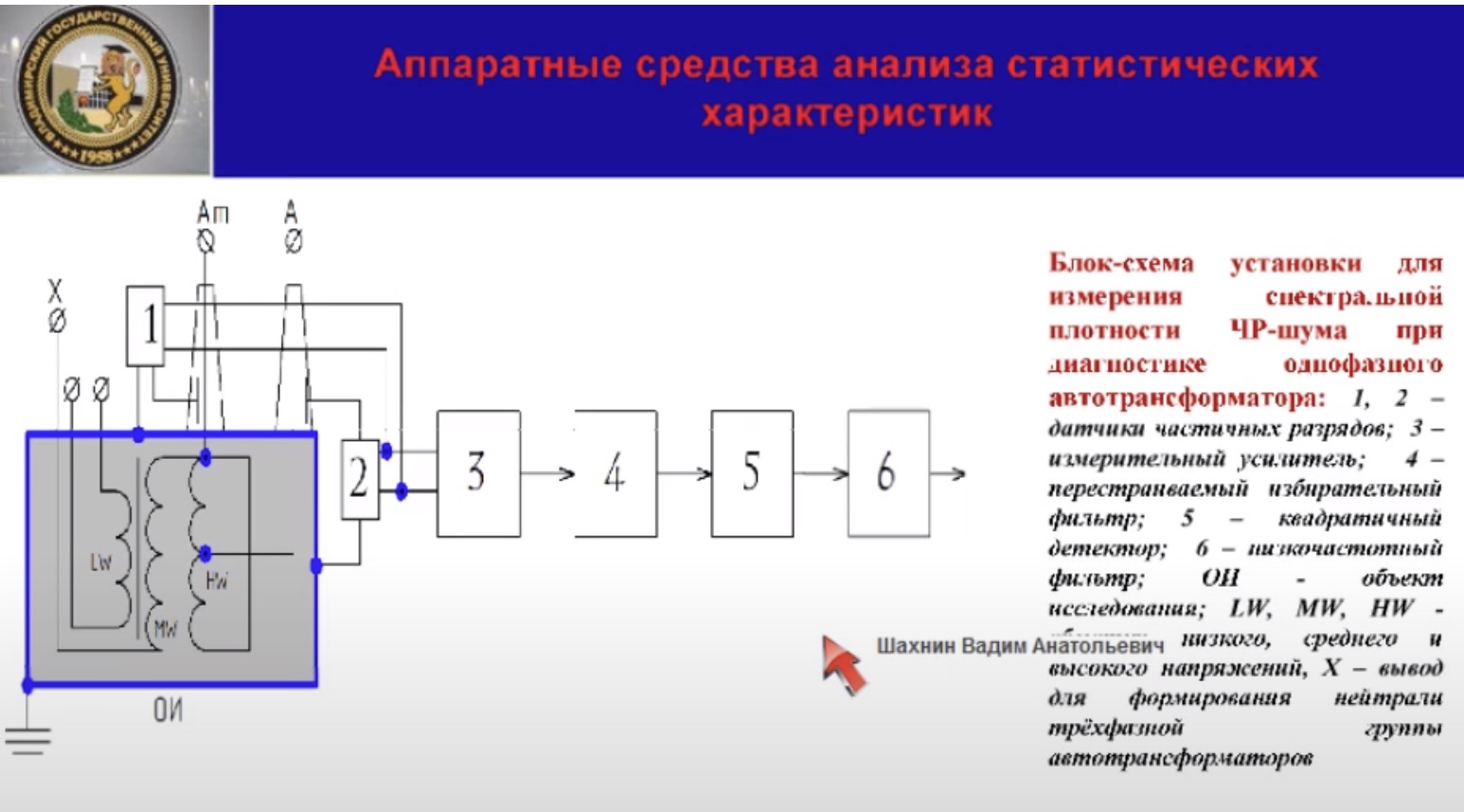
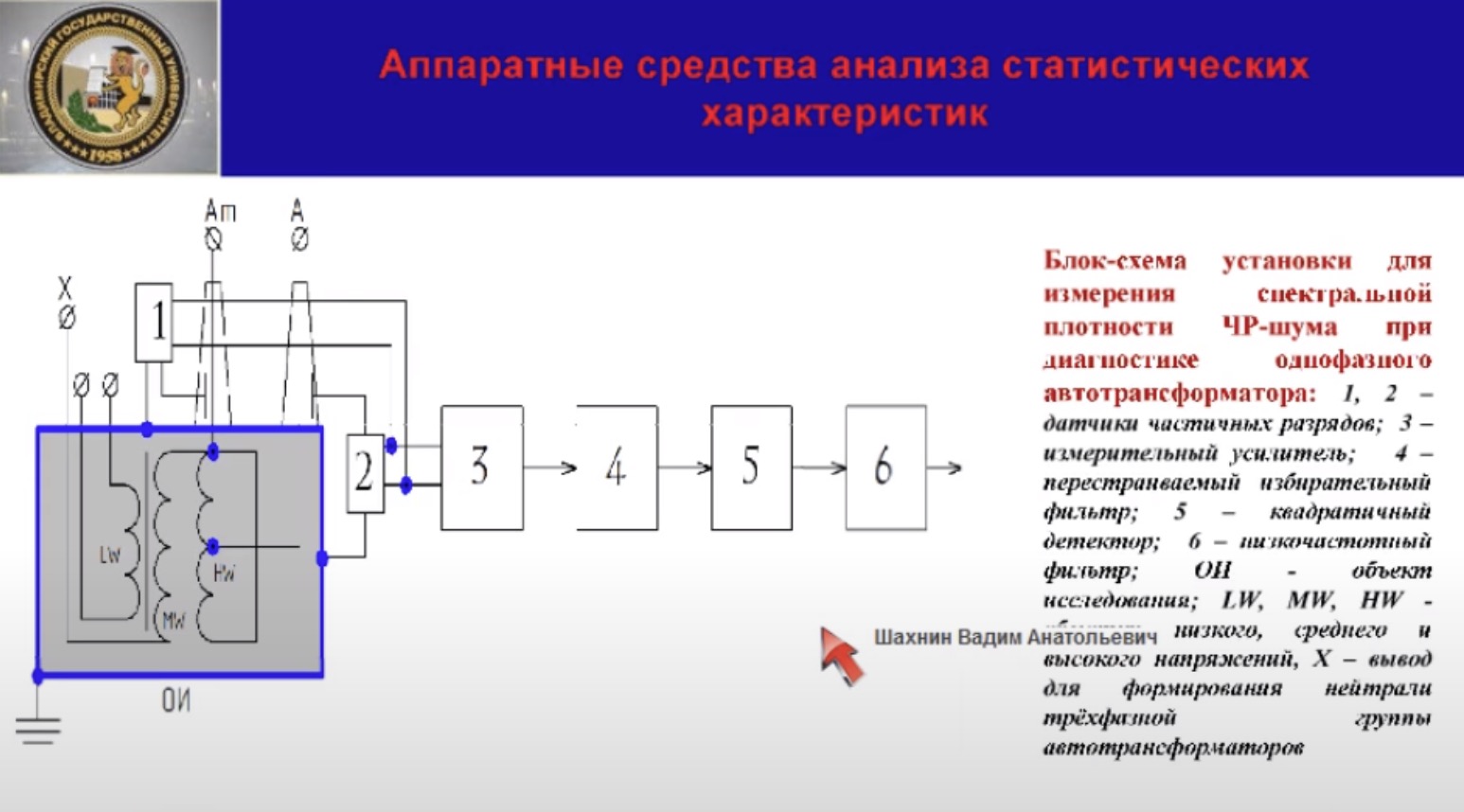
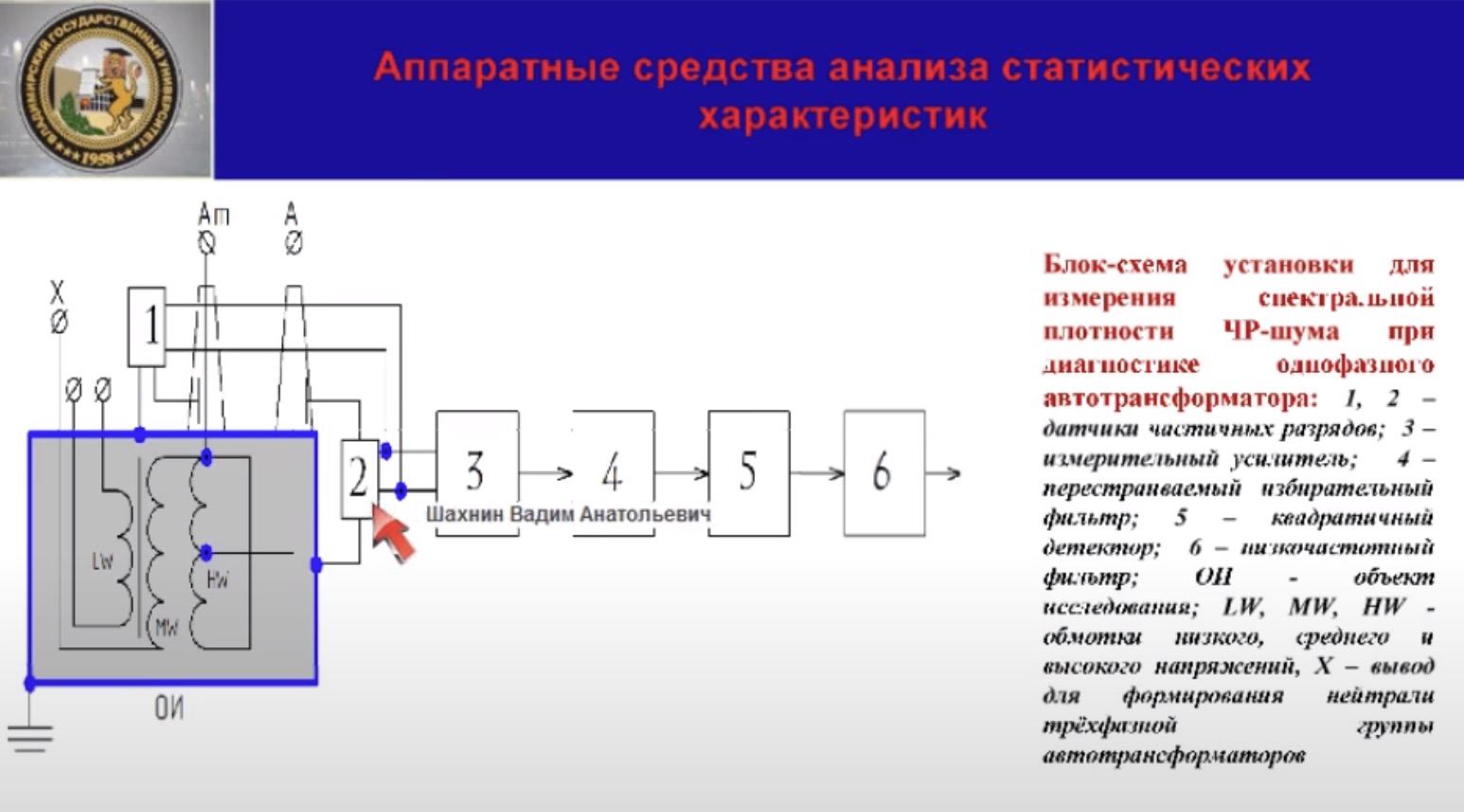
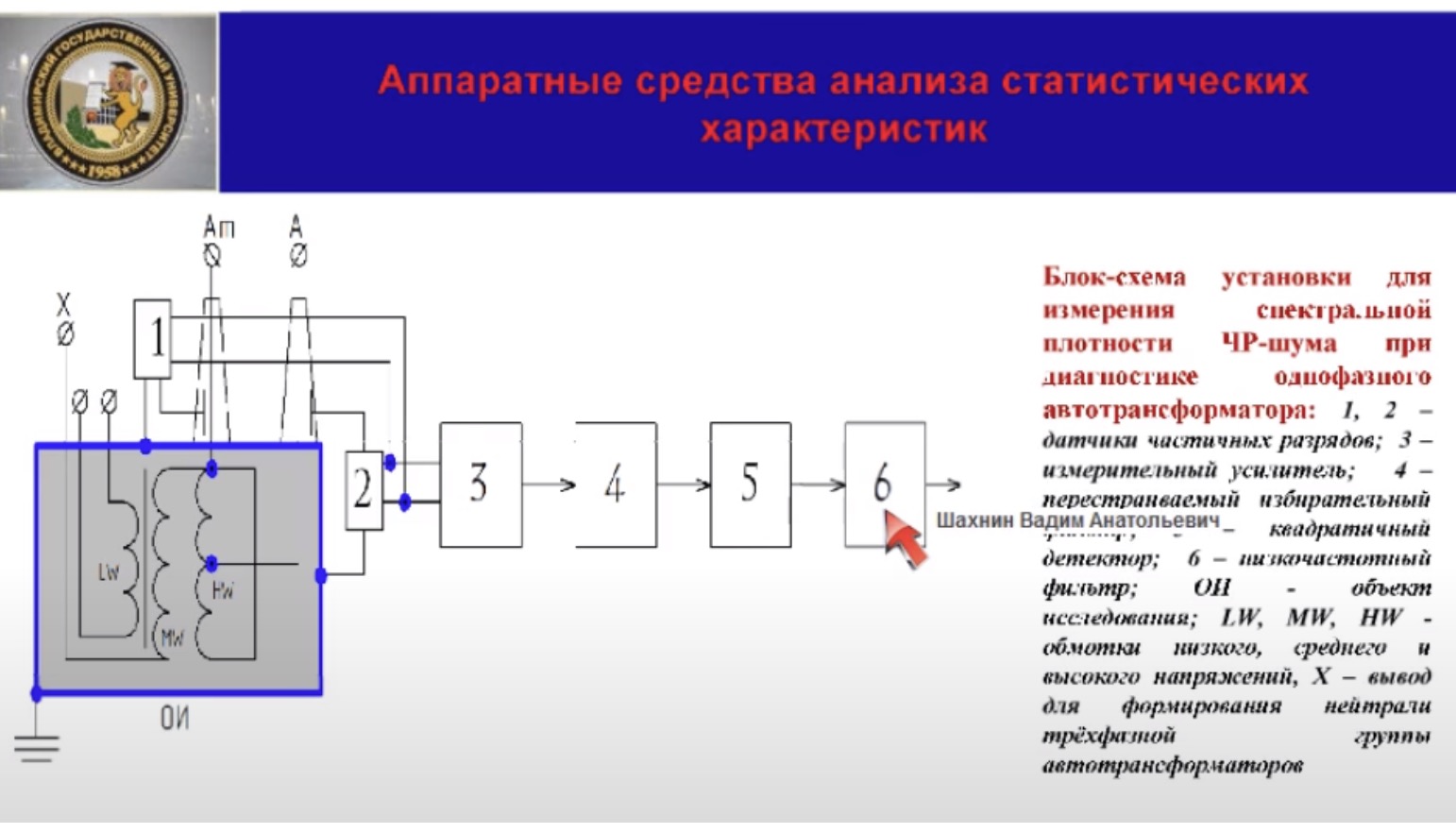
Диагностически для описания случайного процесса хорошо подходит автокорреляционная функция, характеризующая связь между значением случайного процесса в различные моменты времени. Диагностическим принципом состояния изоляции может служить время корреляции шума, вызванного частичными разрядами, определяющих продолжительность временного интервала, в течение которого автокорреляционная функция ещё отличается от 0. Иными словами, это время, в течение которого сохраняется информация о начальном состоянии процесса. Таким образом, автокорреляционная функция является важной диагностической характеристикой при оценке состояния высоковольтного оборудования. Однако, аппаратное определение, инструментальное определение этой характеристики затруднено. Более удобной для аппаратного анализа является спектральная плотность, т. е. распределение по частотам флуктуации состояния изоляции, вызванной частичными разрядами. Как отмечалось выше, согласно теореме Винера – Хинчина, автокорреляционная функция и спектральная плотность стационарного случайного процесса в равной степени описывают этот случайный процесс. Поэтому автокорреляционная функция, действительно, чем шире частота спектра сигнала, чем быстрее происходят изменения в электрическом состоянии изоляции, тем быстрее процесс забывания идёт. С расширением частоты диапазона электрического шума уменьшается время корреляции. Более того, для всех процессов с одинаковой формой спектра и, следовательно, с одинаковым видом автокорреляционной функции, произведение ширины спектра на значение постоянной корреляции является константой. Блок-схема установки для определения спектральной плотности ЧР-шума, диагностированный в высоковольтном аппарате, в данном случае это однофазный автотрансформатор, приведена на слайде. Рассмотрим некоторые особенности аппаратного анализа спектральной плотности шума, обусловленными частичными разрядами. Частичные разряды представляют собой изменение электрического состояния, описываемое с кажущимся зарядом уровня от десятых долей нКл до десятков нКл. Очевидно, что для надёжного определения характеристик шума, вызванных столь незначительными изменениями электрического состояния изоляции, требуется усиление выходного сигнала частичных разрядов. При присутствии в этом сигнале, наряду с шумом, сплошной компоненты спектра, гармоничная составляющая рабочего напряжения – дискретный компонентный спектр создаёт большие экспериментальные трудности в процессе экспериментального анализа частичных разрядов. Дело в том, что интенсивность составляющих, соответственно, дискретных составляющих спектра обычно существенно выше интенсивности ЧР-шума. Это может вызвать, например, нарушение линейности вторичных преобразователей частичных разрядов и другие неудобства. Значительно уменьшить уровень дискретных составляющих обычно удаётся благодаря встречному включению двух идентичных датчиков частичных разрядов, расположенных по разные стороны относительно оси симметрии аппарата на одинаковых расстояниях от него. Дело в том, что, как показывают эксперименты, шум, вызванный частичными разрядами в локальных областях диэлектрика, расположенных на одинаковом расстоянии друг от друга даже в одном бате, мало коррелируемы между собой. Поэтому в спектральной плотности при встречно параллельном соединении датчиков складываются, а сигнал, вызванный дискретными компонентами спектра, вычитается.

18:20
Для анализа частотного распределения шума необходимых выходов усилителя подключить избирательный фильтр с перестраиваемой резонансной частотой. Эффективная частота полосы пропускания должна быть мала по сравнению с деталями анализируемого спектра. Это требует высокой добротности фильтра. Экспериментально установлено, что ширина полосы должна составлять единицы, десятки герц в зависимости от типа изоляции. В этом случае спектральную плотность в полосе пропускания фильтра можно считать постоянной и равной значению этого параметра на резонансной частоте. Если комплексную частотную характеристику блока – измерительный усилитель фильтра обозначить через K(jω), то сигнал на выходе этого блока описывается формулой 13, где волнистая линия указывает усреднение по времени. Для получения сигнала пропорционально измеряемой спектральной плотности применяется квадратичный детектор, подключаемый к выходу избирательного фильтра. Постоянная составляющая выходного напряжения детектора определяет спектральную плотность электрического шума. Для её выделения применяется низкочастотный фильтр. Вернёмся к слайду 9.
19:48
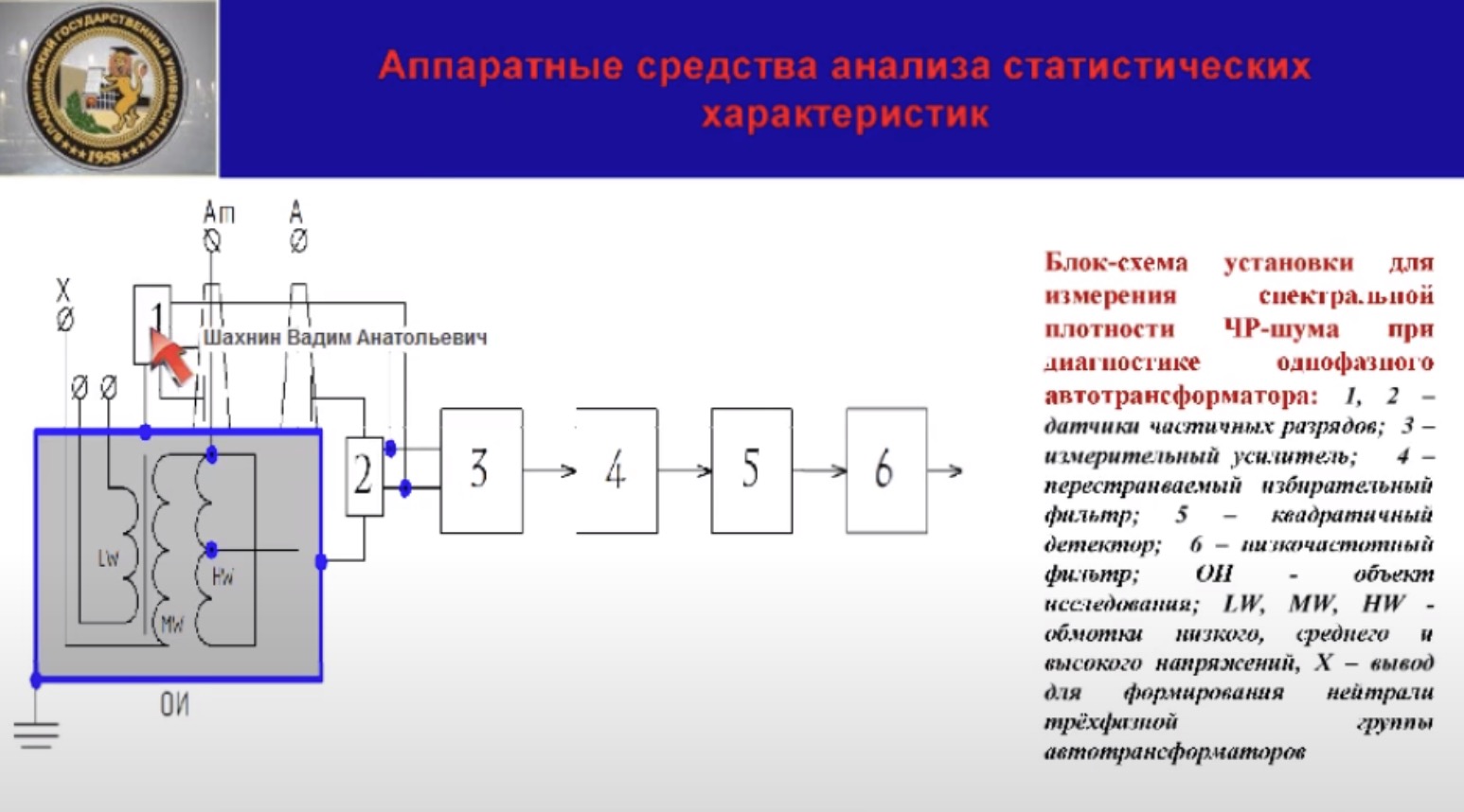
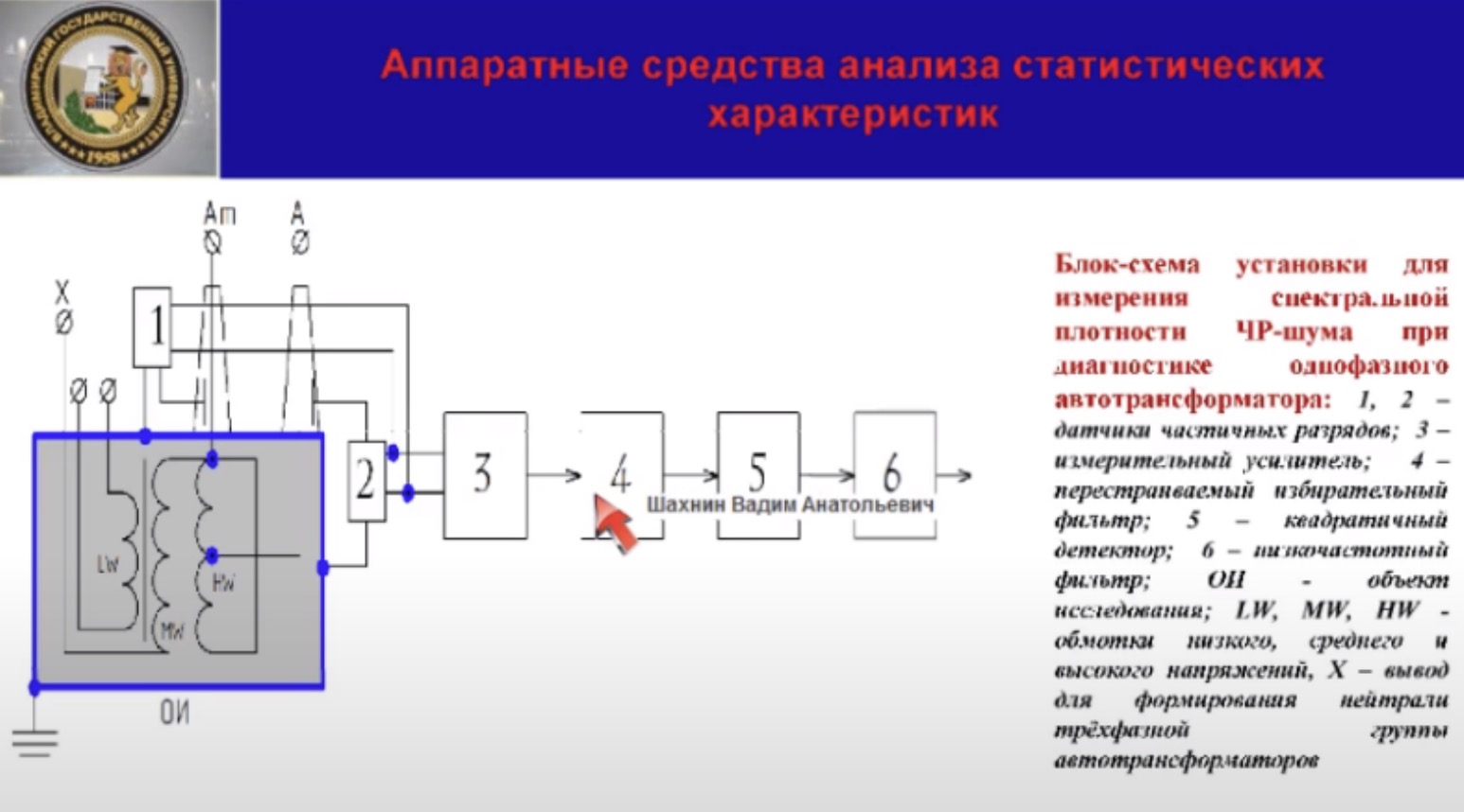
Датчики частичных разрядов 1 и
19:53
2
19:53
как обычно включают специально созданные цепи между измерительными электродами высоковольтных вводов обмотки высокого и среднего напряжения и заземлённым корпусом аппарата. В качестве датчиков мы использовали индукционные датчики HFCT компании HVPD.
20:22
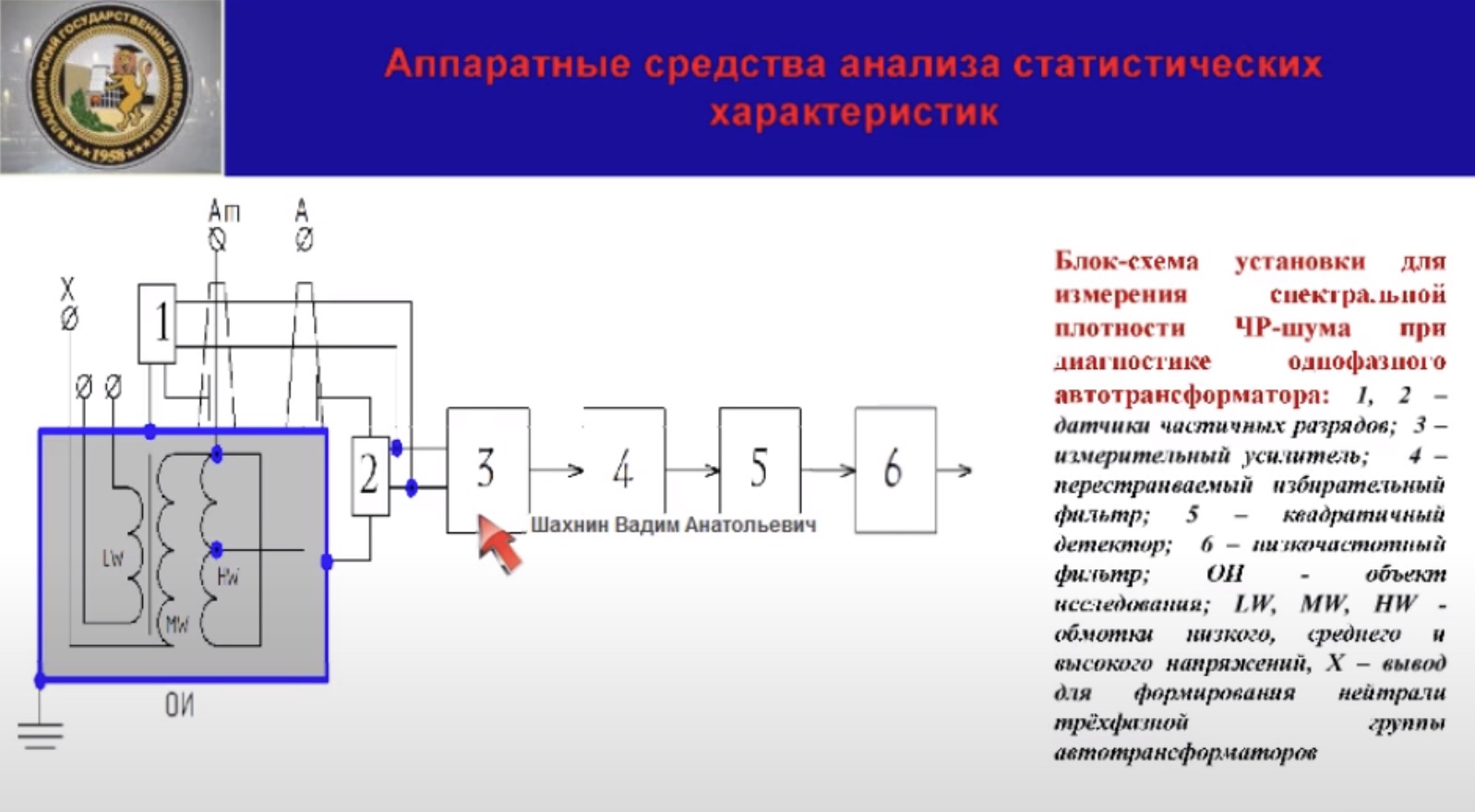
Датчики соединены параллельно встречно и подключены ко входу измерительного усилителя,
20:24
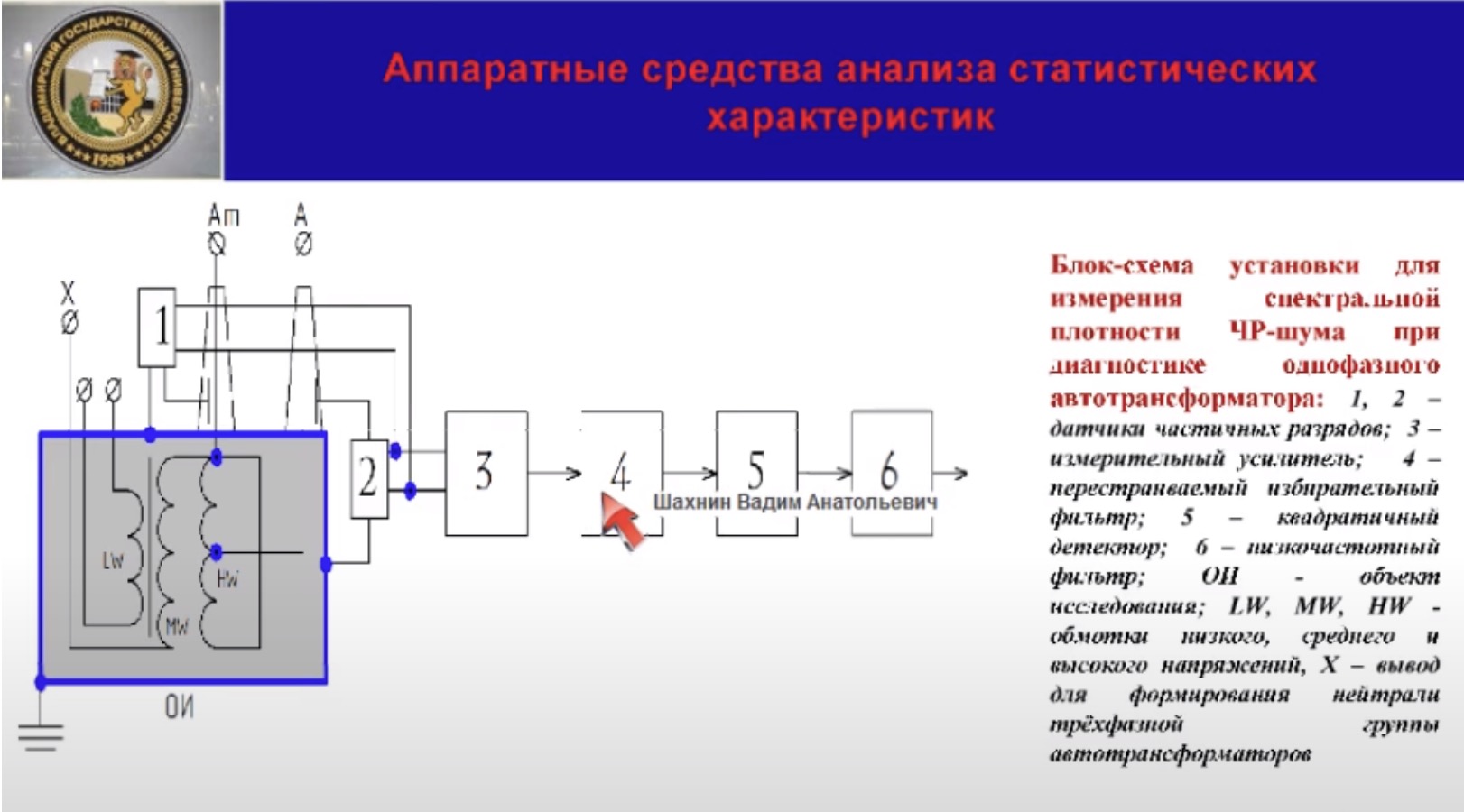
в последовательность которого включены перестраиваемые фильтры, о которых я говорил,
20:24
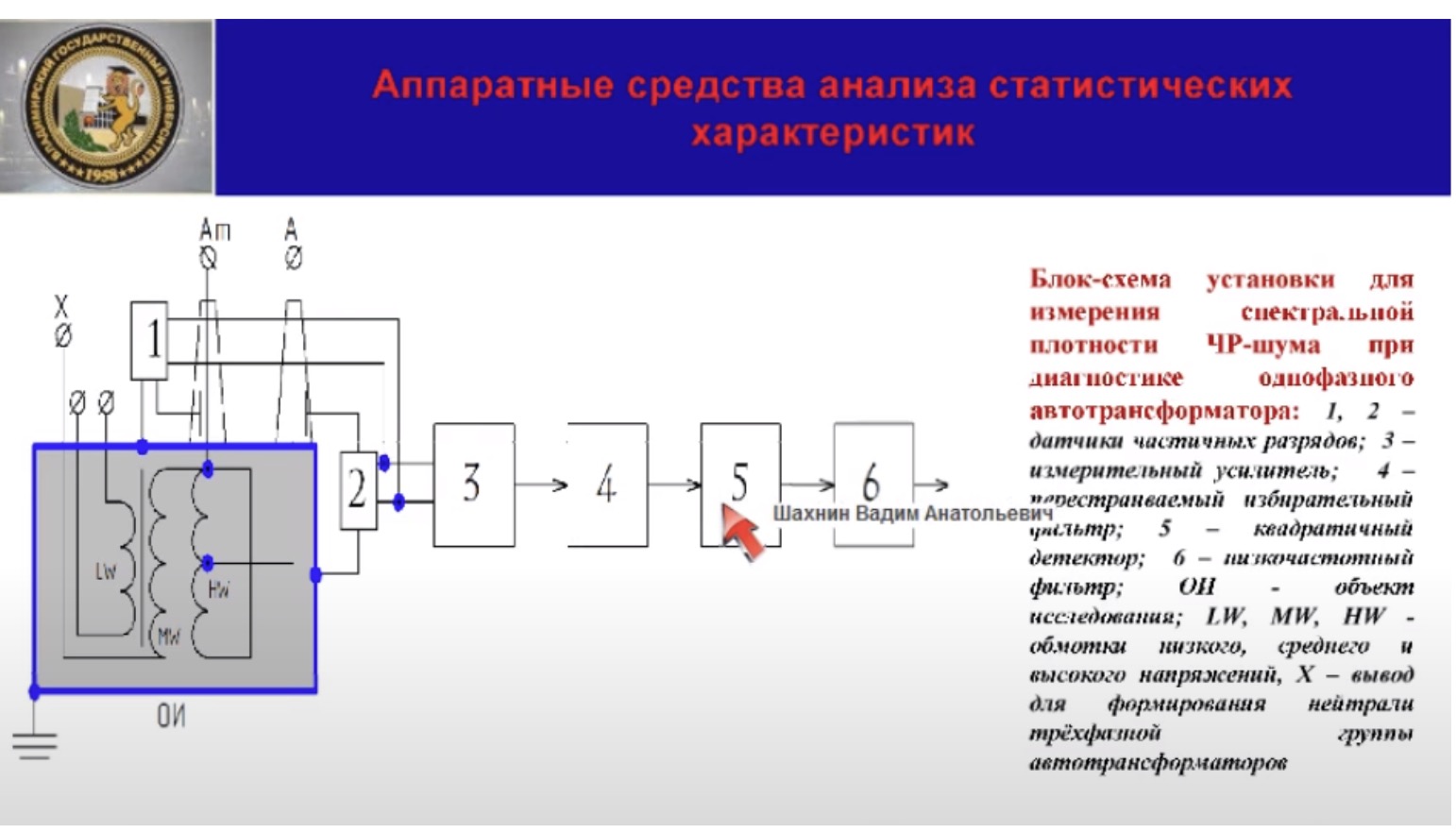
квадратичный детектор
20:26
и фильтр с большой постоянной 20:30 неразборчиво.
20:29
Недостатком установки является то, что она позволяет при достаточно узкой полосе избирательного фильтра измерять спектральную плотность вблизи дискретных компонентов спектра, не обеспечивает возможность измерять шум именно на частотах дискретных компонентов. Поэтому часть информации теряется. Это объясняется тем, что даже тщательная компенсация экранирования не снижает уровень гармонии до уровня шумов. Покажем, что этот недостаток можно устранить, включив между избирательным фильтром 21:05 неразборчиво детектору последовательно соединённый детектор, последовательно работающий в линейном режиме и низкочастотный усилитель. Пусть эффективная полоса пропускания избирательного фильтра существенно меньше диапазона между соседними дискретными линиями спектра и в полосу может попасть только одна гармоническая компонента. В этом случае сигнал на выходе избирательного усилителя состоит из синусоидальной составляющей и шумовой составляющей.

21:38
Последнее слагаемое является случайной величиной с нормальным законом распределения вероятности. Это подтверждается многочисленными экспериментами и соответствует центральной предельной теореме теории вероятности. Суть теоремы заключается в том, что случайная величина, являющаяся результатом воздействия множества случайных факторов при отсутствии доминирования одного или нескольких из них, имеет распределение близкое к нормальному. Для рассматриваемого случая справедливо неравенство 14, где Ec – это действующее значение синусоидальной составляющей,

22:31
а σ – это составляющая, обусловленная случайными частичными разрядами. С учётом нормальности распределения шумовой составляющей, при соблюдении условий 14, справедливо следующее соотношение,

22:48
где I0 – постоянное составляющее выходного тока линейного детектора, а и Iш – это составляющее сигнала, обусловленного флуктуацией низких частот составляющих.

23:02
Таким образом, измеряя I0, можно определить амплитуду спектральной линии,

23:07
а измеряя Iш с помощью квадратичного детектора спектральную плотность шума.

23:12
Абсолютное значение спектральной плотности шума вызвано частичными разрядами и определяется обычно при калибровке измерительной установки по сигналу эталонного генератора белого шума с известной спектральной плотностью. Единицей измерения спектральной плотности является В2/Гц.

23:34
Анализ результатов экспериментальных исследователей ЧР-шумов массовой изоляции автотрансформаторов на установке, представленной на слайде 9, а также результаты подобных исследований для других видов изоляции позволяют представить общую картину спектрального распределения шумов в виде графика, представленного на этом слайде. На кривой спектрального распределения выделены две характерные частоты: 1 и 2, выше и ниже которых наблюдается спад кривой спектральной плотности. Между этими частотами область стабилизации частоты спектральной плотности. Частота 1 обычно увеличивается с ростом частоты приложенного напряжения. В то время как 2 практически не зависит от неё, а определяется физическими свойствами исследуемого диэлектрика. В зависимости от состояния изоляции область стабилизации может быть яркой или слабовыраженной. В первом случае кривая имеет довольно острый максимум. Таким образом, возможно использовать параметры спектрального распределения ЧР-шумов в качестве диагностических признаков при обследовании высоковольтного оборудования. Для реализации этой возможности необходима разработка математических моделей взаимосвязи спектрального сопротивления с параметрами частичных разрядов в диагностируемом диэлектрике. Следует отметить, что одно и то же спектральное распределение может соответствовать различным флуктуационным процессам. И адекватный выбор той или иной модели это, в конечном счёте, вопрос эксперимента. В настоящий момент мы не располагаем достаточно полной картиной о флуктуационных процессах при частичных разрядах в изоляции высоковольтных аппаратов. Однако, можно сделать некоторые замечания в пользу выбора той или иной модели. Дальнейший анализ проводим, базируясь на следующих положениях. Во-первых, будем рассматривать шумы, вызванные частичными разрядами под действием рабочего напряжения высоковольтного аппарата и считать, что постоянные явления изменения электрических величин, сопровождающих частичные разряды, много меньше периода изменения электрического поля от 20 мс. Другими словами, мы полагаем, что динамика процессов при циклическом изменении электрического поля с частотой 50 Гц совпадает с динамикой квазистатического изменения поля. Во-вторых, к каждому из процессов изменения электрического состояния изоляционной среды соответствует своя компонента сигнала датчика частичных разрядов. Именно обратимым процессам соответствуют компоненты, изменяющие такт с изменением внешнего воздействующего поля, а необратимым – скачкам, связанных с частичным разрядом, соответствуют импульсные компоненты с продолжительностью гораздо меньшего периода. Очевидно, что при наличии математической модели, адекватно описывающей статистические характеристики частичных разрядов, является необходимой предпосылкой при разработке электрошумовых методов интродиагностики. Наиболее простым подходом к расчёту спектра частичных разрядов является рассмотрение задачи о наложении независимых импульсов. Предположим, что при равномерном изменении напряжённости внешнего электрического поля в диэлектрике возникает последовательность статистически независимых частичных разрядов, каждый из которых вызывает на выходе датчика ЧР сигнал, который можно описать вот этой формулой.

27:13
Упрощая задачу, будем считать, что форма импульса всех частичных разрядов в исследуемом диэлектрике за период приложенного напряжения одинакова, и что вероятность возникновения импульса на интервале пропорциональна длительности этого интервала, т. е. что процесс пуассоновский. Эта модель предполагает полную равноправность всех частичных разрядов в диагностируемом аппарате. Так что в процессе частичных разрядов с равной вероятностью участвуют все локальные области диэлектрика 27:47 неразборчиво высоковольтного аппарата. Причём частичные разряды случайным образом могут заменять друг друга. Задача, с точки зрения теории вероятности, сводится к определению флуктуации числа скачков за единицу времени. Сигнал датчика, с учётом этого, можно описать формулой 15,

28:04
множество этих импульсов на выходе датчика. Пусть форма приблизительно задаётся экспоненциальной функцией 16,

28:15
тогда с использованием математического аппарата, о котором я говорил в первой части вебинара, формула для спектральной плотности будет иметь вид, представленной уравнением 17.

28:30
На частоте , близкой к , а – это приблизительная величина обратно пропорциональная длительности импульса. Спектральная плотность, можно сказать, постоянная. На частоте ω=λ спектральная плотность убывает вдвое, и эта частота может быть принята за верхнюю границу спада спектра электрического шума.

28:52
Длительность импульсов , это приблизительно 1, определяется физическими свойствами диэлектрика и внешним воздействиям.

29:07
В твёрдой изоляции значения этого параметра лежат в диапазоне 10-9, 10-8 секунд, а в жидкой и газовой на уровне 10-9, 10-5 и 10-6. Эксперименты показывают, что вычисления спектральной плотности в области плато по формуле 17

29:28
совпадают по порядку величины с результатами измерений, в частности, на установку, представленной на слайде 9. Однако, модель, рассмотренная выше, не позволяет объяснить низкочастотный спад спектральной плотности

29:41
и наличие частоты 1. Очевидно, что это связано с гипотезой о независимости частичных разрядов. Один из путей учёта взаимодействия между отдельными частичными разрядами, то есть корреляции между ними, формально сводится к тому, что для пуассоновского импульсного процесса распределения интервалов времени между последовательными частичными разрядами задаётся экспоненциальной функцией. Мы воспользовались этим приёмом. Экспериментально была получена эмпирическая формула

30:14
для плотности распределения интервалов времени , разделяющая два следующих друг за другом импульса частичных разрядов. И, использую эту формулу, мы получили модернизированную модель, которая описывается уравнением 19.

30:34
По сравнению с 17, модель 19 более адекватно описывает шумовой процесс, поскольку содержит поправочный множитель, обуславливающий некоторый спад спектральной плотности ЧР-шума в области низких частот.
30:56
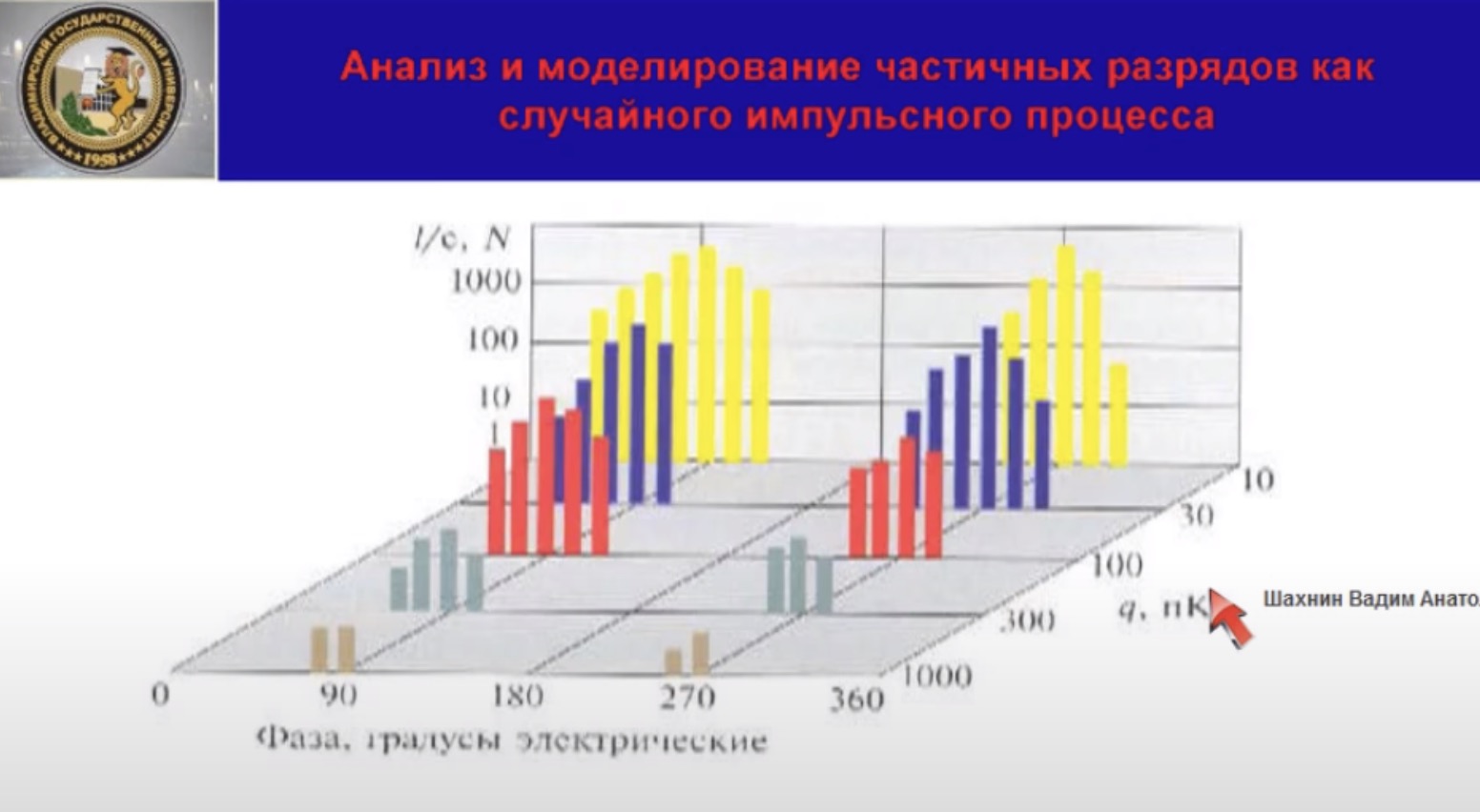
Вместе с тем эта поправка не исчерпывает вопроса о поведении спектральной плотности в области низких частот. Распределение числа частичных разрядов по кажущимся зарядам и по фазе воздействующего напряжения неравномерно. Это установлено многочисленными экспериментами, в частности, на этом слайде, мы показываем рисунок, также заимствованный из книги Удовико. На нём представлены результаты, полученные при постепенном увеличении амплитуды воздействующего напряжения. Таким образом, рассматриваемый шумовой процесс, т. е. процесс частичных разрядов, нельзя считать стационарным, т. к. существует взаимосвязь между вероятностными характеристиками процесса и временем (распределение по фазе логично распределению во времени в течение периода). Однако, многочисленные измерения, в том числе проведённые нами, на установке, показанной на слайде 9, показывают, что спектральная плотность на частоте равной 0 обращается в 0. А теоретически известно, что выполнение условия равенства нулю спектральной плотности на нулевой частоте характерно на стационарность или периодическую не стационарность процесса. С учётом изложенного, логично предположить, что процесс частичных разрядов при периодическом воздействии напряжения является периодически нестационарным. Покажем, что предлагаемая модель адекватно отражает вышеизложенные теоретические и экспериментальные результаты. То, что для этой модели выполняются условия равенства нулю спектральной плотности на нулевой частоте. Для этого выразим спектральную плотность через реализацию случайного процесса.

32:57
Опять же, с использованием вышеизложенного математического аппарата, на который я ссылался раньше, получена формула 20.

33:05
Для частоты, равной 0, выражение 20 поменяет форму 21.

33:13
Интеграл в последнем выражении пропорционален изменению заряда за период приложенного напряжения. Эта величина не может превышать значение кажущегося заряда при полном пробое изоляции. Следовательно, спектральная плотность на нулевой частоте равна 0, что подтверждает адекватность предлагаемой модели 19, и позволяет её использовать при анализе результатов диагностики высоковольтного оборудования по параметрам частичных разрядов.
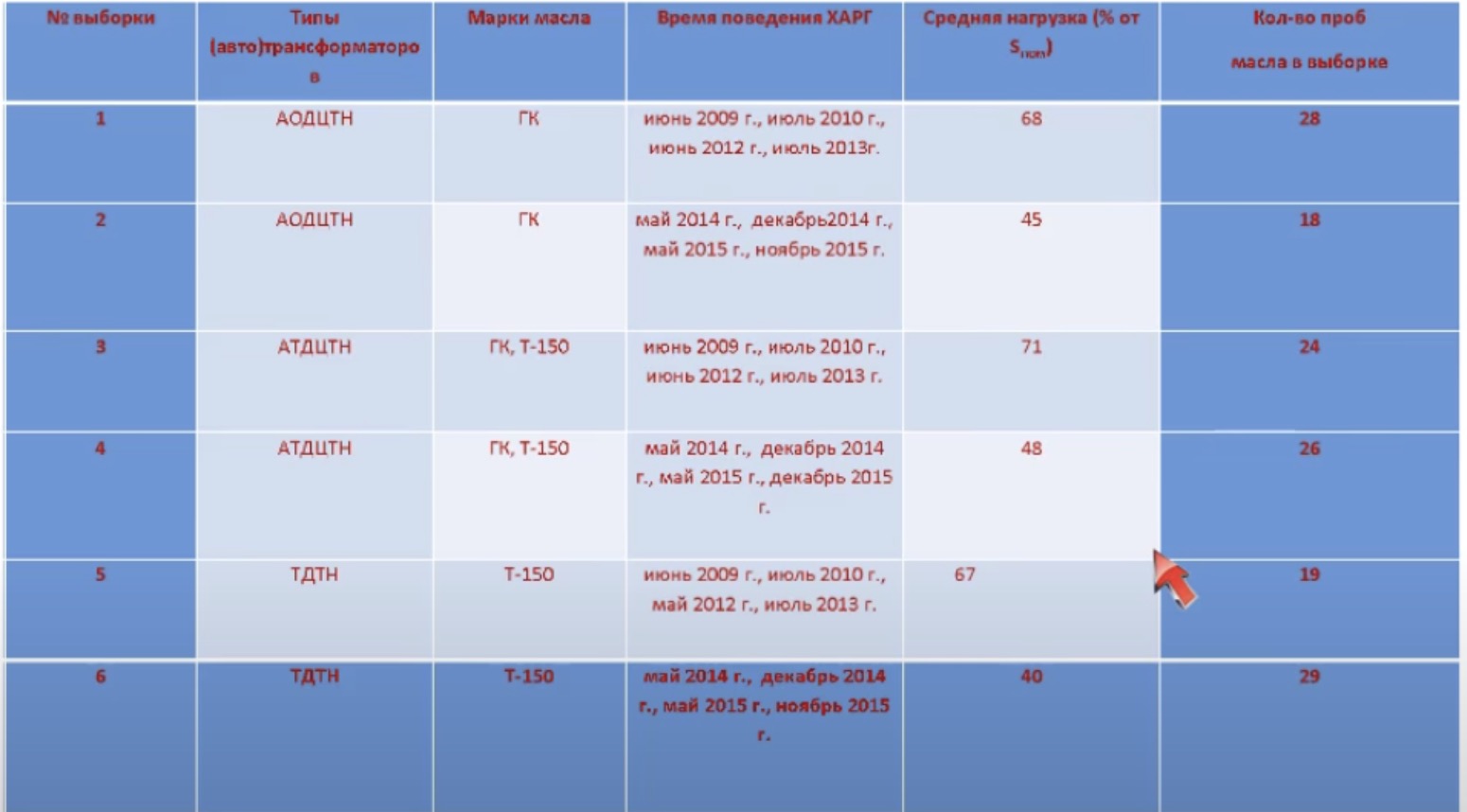
На следующих четырёх слайдах представлены результаты, подтверждающие целесообразность применения спектральной плотности при диагностике изоляции высоковольтного оборудования, в частности, для оценки и концентрации растворённых газов.
33:43
33:48
33:49
33:51
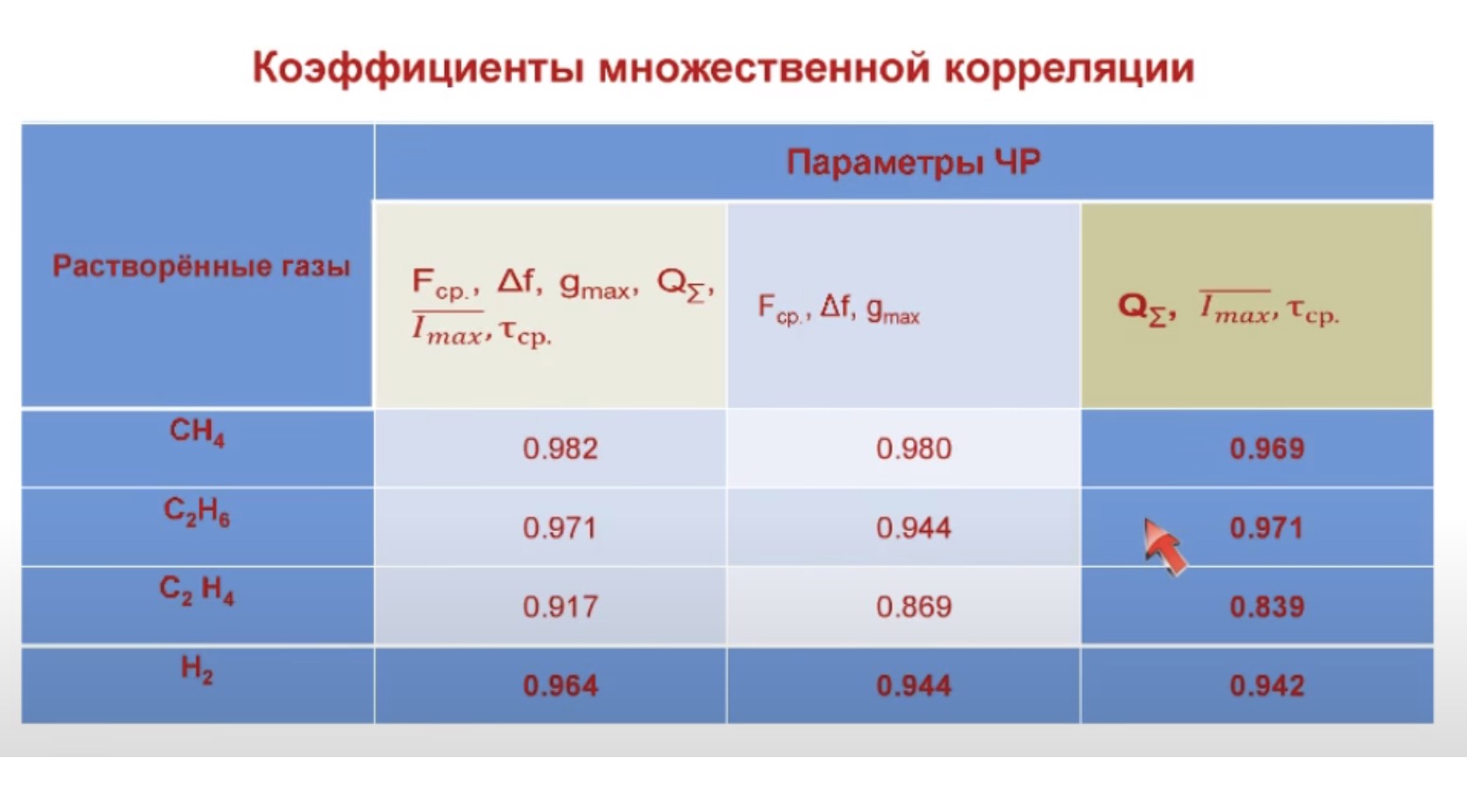
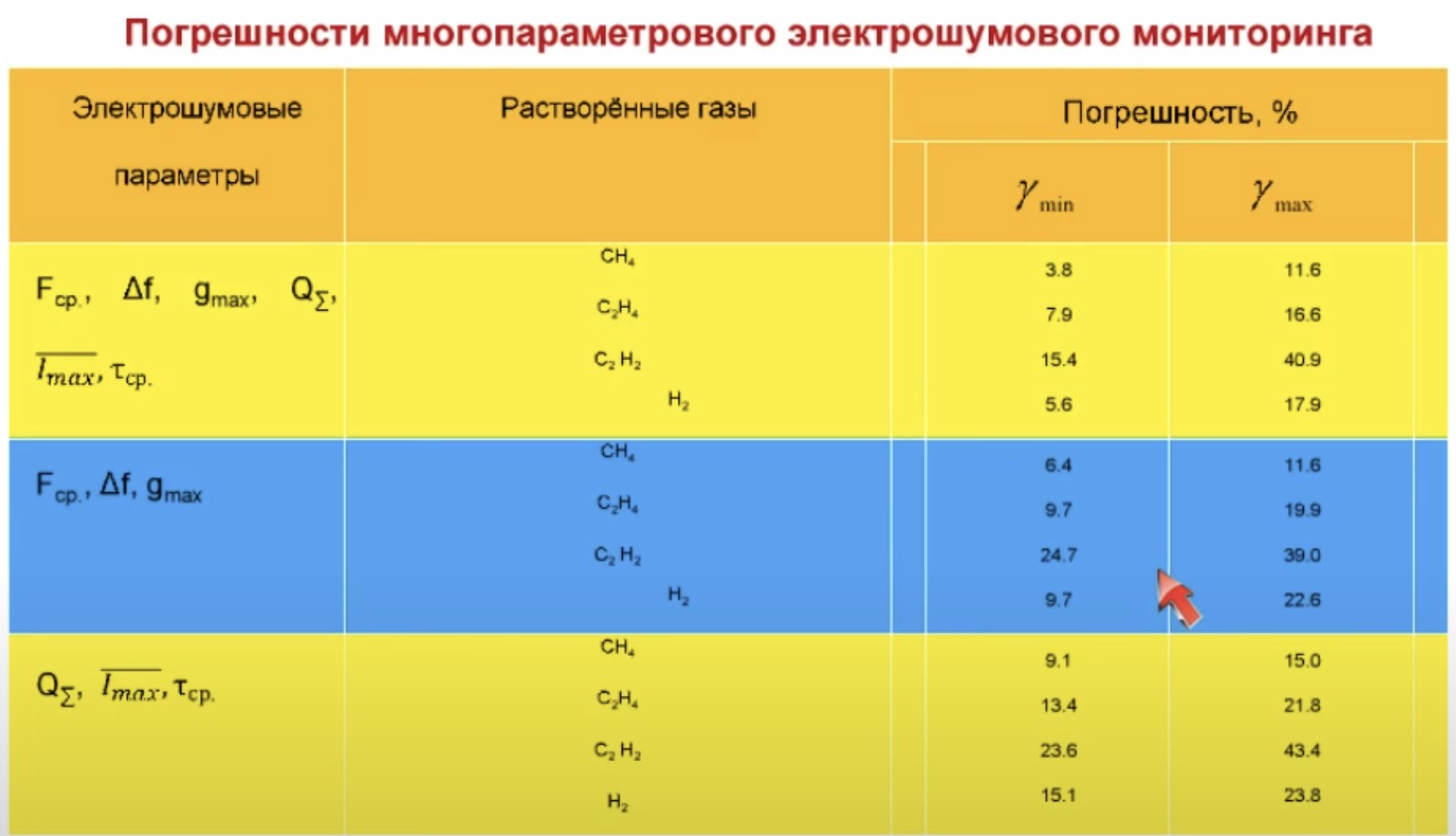
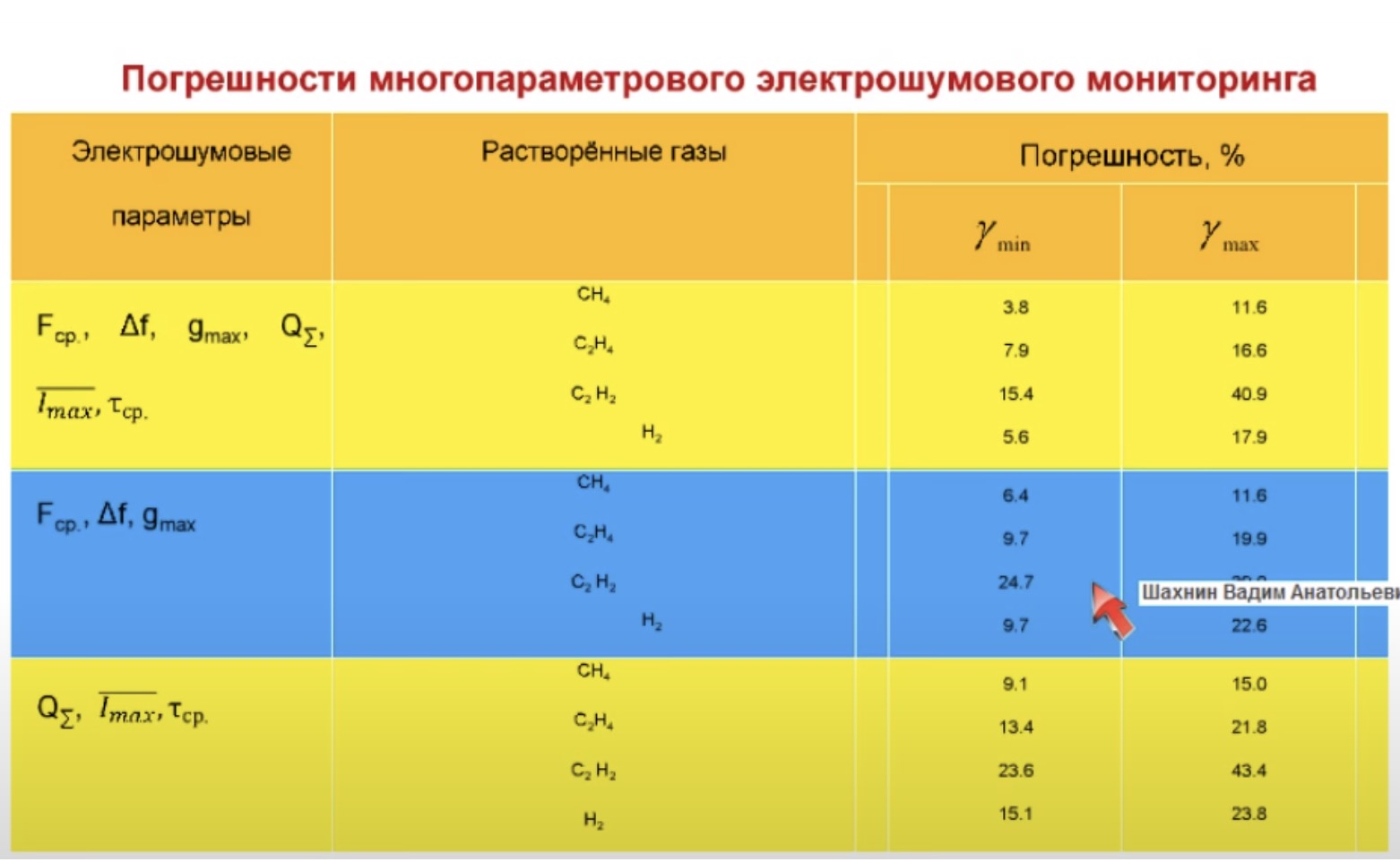
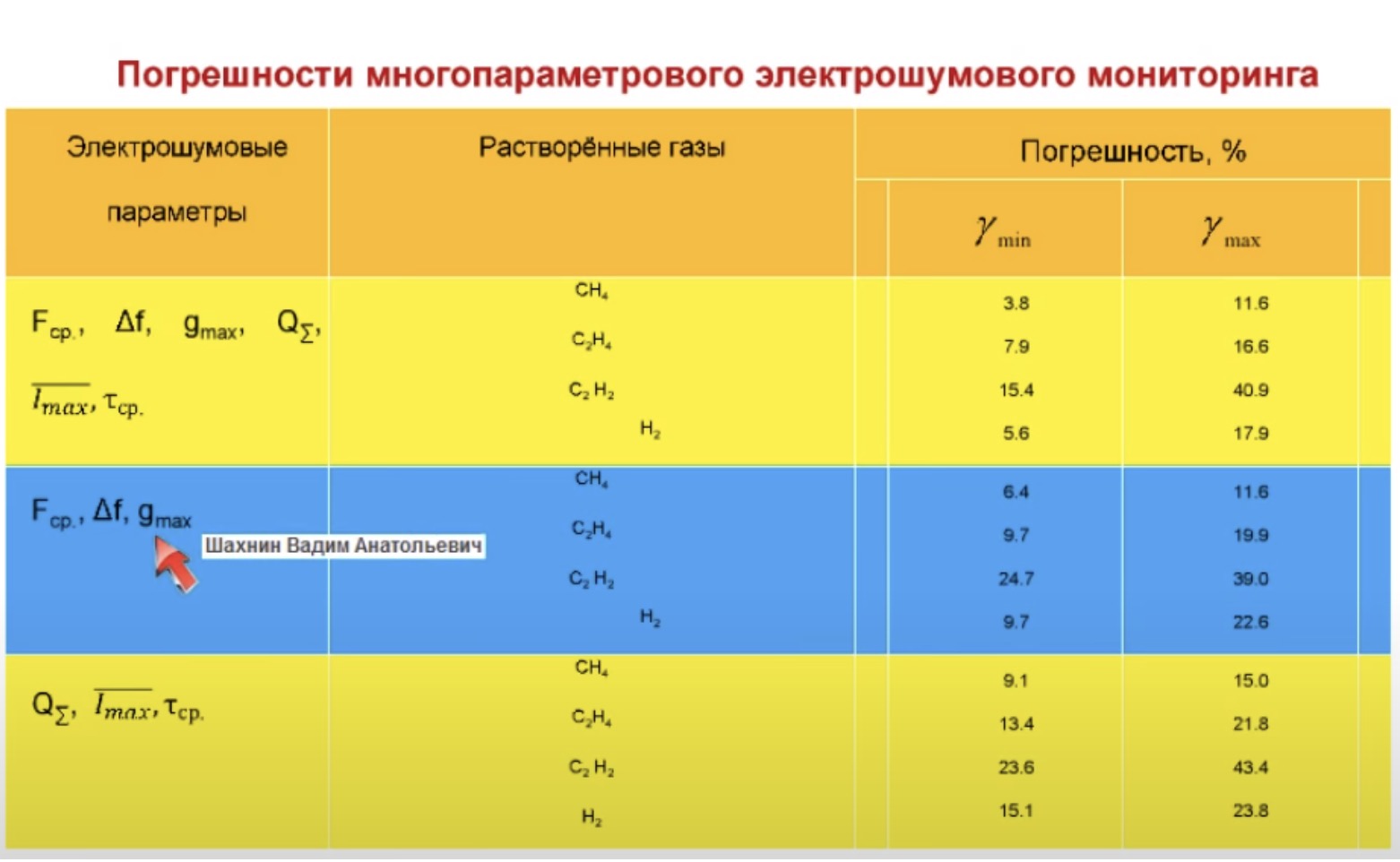
Об этом я говорил на предшествующем вебинаре. В фрагменте на слайде, выделенным синим цветом, представлены погрешности оценки концентрации растворённых газов (метан, этилен, этан и водород) в изоляции высоковольтных аппаратов при использовании для диагностики параметров спектральной плотности.
34:32
Что это за параметры?
34:41
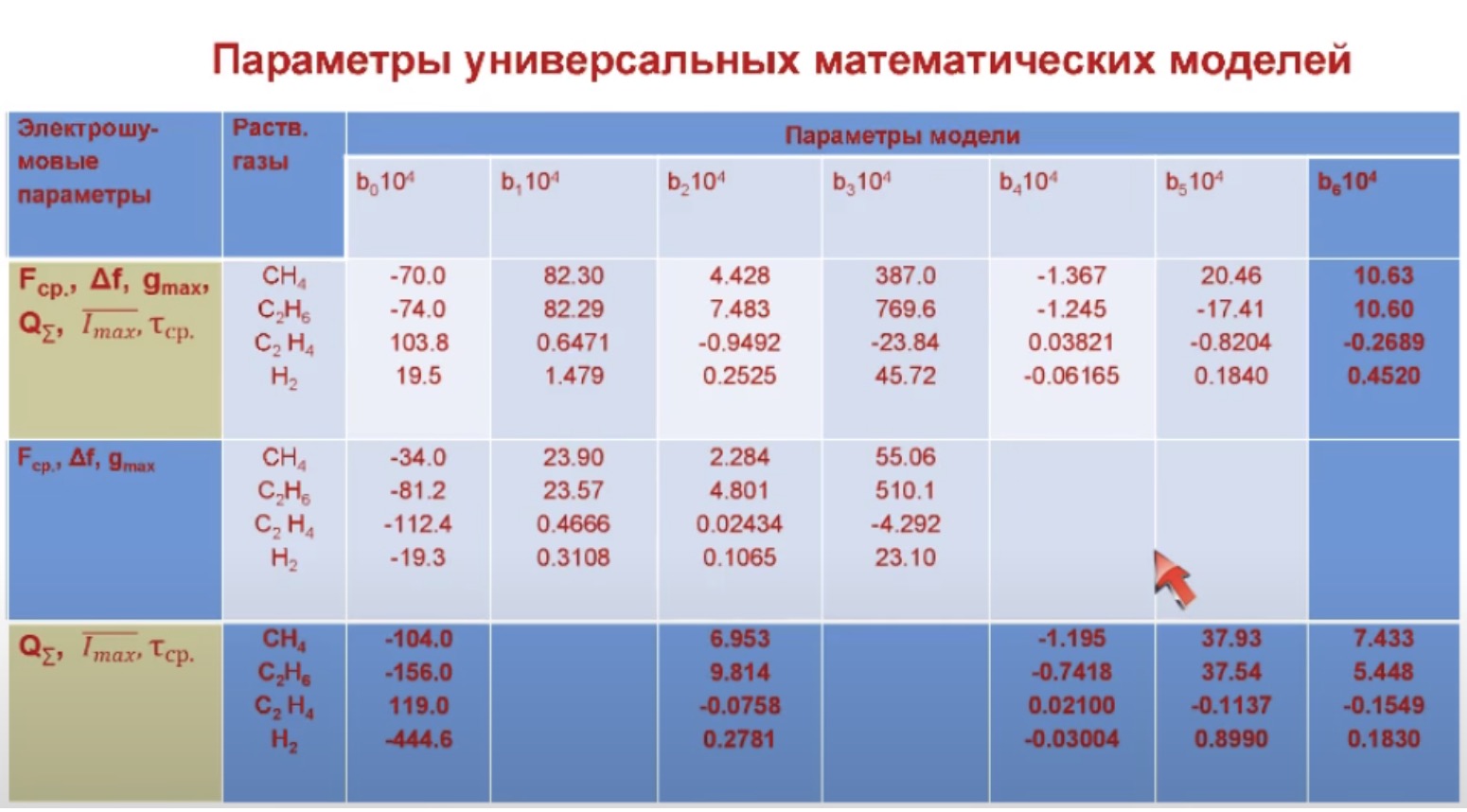
Это максимальное значение спектральной плотности, частотный диапазон спектральной плотности и средняя частота на этом диапазоне. Этот слайд иллюстрирует, что погрешности определения оценки концентрации растворённых газов находятся на уровне современных применяемых методов и могут быть использованы на практике. На этом моя часть вебинара закончена. Спасибо за внимание. Прошу вопросы.
– Вадим Анатольевич, спасибо за доклад. Уважаемые участники, если у вас есть вопросы, пожалуйста, задавайте их в чат. Мы подождём ещё пару минут. Если они не появятся, то мы будем заканчивать. Хотел сказать, что уже доступна часть предыдущего вебинара с Вадимом Анатольевичем Шахниным. Ссылку в чат я уже отправил. Пожалуйста, заходите, смотрите. И напомню, что у нас планируется насыщенная программа вебинаров с Вадимом Анатольевичем. Пожалуйста, регистрируйтесь, и ничего не пропустите. Я ещё раз продублировал ссылку в чат на новости на сайте, на котором публикуются анонсы вебинаров. Пожалуйста, добавьте в закладки, чтобы ничего не пропустить. Пока вопросов нет. Вадим Анатольевич, может быть вы поделитесь с нами информацией о грядущих вебинарах? Что будет на следующих вебинарах, которые будут в ноябре, декабре?
– Я планирую перейти к более подробному рассмотрению оборудования для дистанционной диагностики. Особенность метода диагностики на основе частичных разрядов – это возможность дистанционного анализа параметров и характеристик. Ясно, что частичные разряды сопровождаются изменением электромагнитного поля и с использованием общеизвестных антенн, и используются обычно для анализа радиошумов. Возможность дистанционной диагностики высоковольтного оборудования электрических подстанций. Какие тут преимущества? Если использовать этот метод, то, обеспечивая перемещение антенны, можно производить диагностику с помощью одного и того же комплексного оборудования всех высоковольтных аппаратов подстанции. Особенность заключается в возможности перемещения антенны. Мы разрабатываем ещё и приводы перемещения антенн. Устройство становится мехатронным. Идея такая, что вдоль забора подстанции расположена роликовинтовая передача с вращающимся винтом, по которой перемещаются антенны и другое оборудование для анализа частичных разрядов. Обычно высоковольтные аппараты расположены как раз в пределах досягаемости этой антенны, и таким образом мы обеспечиваем дистанционность оборудования. Сейчас мы пытаемся включиться в план 38:32 неразборчиво ПАО «Россети» именно с таким предложением. Примерно на одно региональное предприятие 38:43 неразборчиво. Одного такого комплекса бывает достаточно. Вот такие у нас планы. Развитию этого метода диагностики, перспективе этого внедрения будут посвящены следующие вебинары.
– Вадим Анатольевич, спасибо. Вопросы так и не появились в чате. Поэтому думаю, можем заканчивать. Уважаемые участники, благодарим за участие. Регистрируйтесь на новые вебинары. До скорых встреч! До свидания!
– Спасибо. До свидания!
Регистрируйтесь на вебинары проекта Test-energy.ru
Смотрите видеозаписи прошедших вебинаров проекта Test-energy.ru
Если вам нужна профессиональная консультация по вопросам измерения и анализа частичных разрядов или требуется подбор оборудования для вашего конкретного случая, то заполните форму:
Смотрите также:


















